Nebojte se 3D grafů

Program se jmenuje 3D Grapher. Po jeho stažení jej nainstalujte - a můžete se pustit do tvorby.

Než půjdeme dál, omlouváme se všem, kdo jsou s matematikou kamarádi. V dalším výkladu totiž budeme hodně zjednodušovat a vysvětlovat i věci, které oni jistě dávno vědí.

Lehký úvod do 3D grafů

Když chceme kreslit grafy ve třech rozměrech - tedy 3D - budeme potřebovat 3 osy - vodorovnou X, svislou Y a vodorovnou osu Z mířící od nás do dálky (do hloubi monitoru). Pravdou ovšem je, že v Grapheru je možné osy různě natáčet, takže nakonec může být vodorovná třeba i osa Y.

Když si graf představíme jako spoustu malých teček v prostoru, pak matematický zápis grafu říká, jak spolu souvisejí souřadnice x, y a z každého bodu. Když tedy například platí x = y = z, pak je grafem plocha v prostoru, která je tvořena například body 1,1,1 nebo 2,2,2 nebo 6,6,6. Když chceme, aby graf nevypadal jako placka, musíme použít nějaký o trochu složitější vzorec - nějakou nelineární funkci, například x^2 nebo sin x.

Jdeme kreslit

Nyní vytvořme první graf. Napište do horního okna Grapheru následující 3 řádky:

rgb(1,1,0)

crt(x,y,z)

y = z = x

První řádek určuje barvu grafu (3D obrázek ale bude nakonec stejně černobílý), v tomto případě se míchá r + g (red = červená, green = zelená) a vzniká tedy žlutá. Hodnoty trojice základních barev se mohou pohybovat mezi 0 a 1.

Druhý řádek říká, že budeme kreslit graf pro trojici os x, y a z a zároveň nastavuje standardní rozpětí grafu - od - 5 do 5 (pro hodnoty v tomto rozmezí se budou počítat jednotlivé body grafu). A konečně třetí řádek je rovnicí samotného grafu - té plochy, o které již byla řeč výše.

Nyní stačí stisknout klávesu F5 (nebo v menu zvolit Project/Graph) a graf se vykreslí. Chcete-li graf vidět ve 3D, zvolte View/Eyes/Anaglyph. Doporučujeme však ještě před tím změnit v menu Options/Graphing/Anaglyph barvu pro levé oko na červenou a pro pravé na zeleno-modrou (má zelenou a modrou složku s hodnotou 255, červenou 0). A v menu Options/Graphing/Eyes nastavte vnímání hloubky (Depth Perception) pro Anaglyph na první čárku zleva.

Po vykreslení můžete šipkami v okně Rotate View otáčet obrazem okolo libovolné osy. Pokud na nějakou šipku dvojkliknete, graf se bude sám otáčet v prostoru. S 3D brýlemi to u některých grafů bývá skutečně velmi pěkný pohled.

Lepší obrázky

A nyní pojďme ke složitějším grafům. Pokud do kódu pro náš první graf přidáte další řádek, například z = 5, přibude další plocha (její souřadnice z bude 5, ostatní se budou měnit od -5 do 5). Můžete přidat i více podobných řádků, například z = 2, z = -2, x = 5 - a plochy se nám dále rozmnoží.

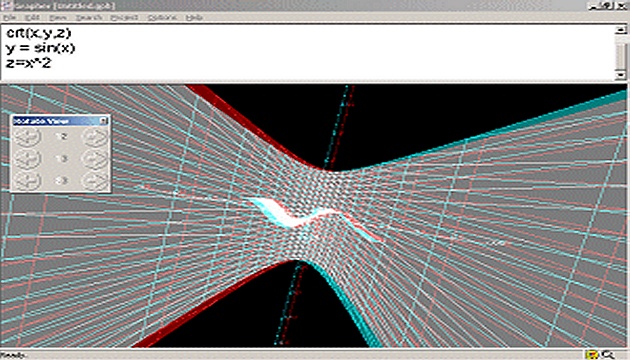
Jestli už vás rovné plochy nebaví, zkuste rovnici y = sin(x). Objeví se zvlněná plocha. Přidáte-li ještě řádek z = cos(x), budete mít kolmo na ni další zvlněnou plochu. Když místo druhého řádku napíšete z = x ^ 2, souřadnice z se vám odváže - bude růst (i klesat) daleko rychleji než x, takže i výsledný graf bude poměrně značně odlišný od svých předchůdců - a 3D efekt velmi výrazný.

A nyní již nastává čas pro vaše experimenty. Pokud vás nic nenapadá, zkuste třeba rovnice z=x*sin(x)^2, z=x^3*sin(x)^2 nebo z=x^3*sin(x)^3. Automatické rozpětí souřadnic od -5 do 5 lze nastavit nejen výrazem crt(x,y,z), ale i tímto: var x = -5 to 5 step 20 (poslední hodnota udává, po kolika krocích se dojde od -5 do 5). Chcete-li nastavit jiné rozpětí, máte samozřejmě možnost.

Součástí programu je i poměrně rozsáhlá nápověda. Je sice v angličtině, ale i ten, kdo tento jazyk neovládá, v něm jistě při troše pátrání nalezne užitečné informace - například o použitelných funkcích.